Reflections common core geometry homework answers – Dive into the realm of reflections in Common Core geometry homework answers, where fundamental concepts, practical applications, and intricate transformations intertwine. This comprehensive guide unravels the mysteries of geometric reflections, empowering learners to master the intricacies of this fascinating subject.

Within these pages, you will embark on an enlightening journey through the core principles of geometric reflections, uncovering their significance in everyday life and various disciplines. Prepare to unravel the captivating properties of reflections, delve into their role in geometric constructions, and witness their transformative power in creating new shapes.

Geometric Reflections

Geometric reflections are transformations that create a mirror image of a figure across a line, plane, or point. Reflections play a crucial role in geometry and have numerous applications in real-world scenarios.

Types of Reflections: Reflections Common Core Geometry Homework Answers

• Point Reflection:Reflects a figure across a single point, creating a mirror image with the same size and shape.
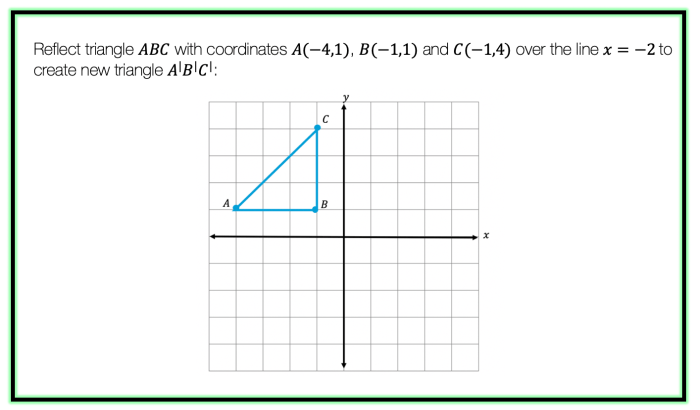
• Line Reflection:Reflects a figure across a line, creating a mirror image with the same size and shape, but flipped along the line.
• Plane Reflection:Reflects a figure across a plane, creating a mirror image with the same size and shape, but flipped across the plane.

Reflection Properties

Reflections preserve certain geometric properties:

• Distance:The distance between two points remains the same after reflection.
• Angles:The measure of angles remains the same after reflection.
• Shape:The shape of a figure remains the same after reflection.

Transformations

Reflections can be used as geometric transformations to create new shapes:

• Translation:Moving a figure without changing its size or shape.
• Rotation:Turning a figure around a fixed point.
• Dilation:Enlarging or shrinking a figure.

Coordinate Transformations

Reflections can be represented as coordinate transformations:

• Point Reflection:(x, y) → (-x, y)
• Line Reflection:(x, y) → (x, -y)
• Plane Reflection:(x, y, z) → (-x, -y, -z)

Symmetry

Reflections play a role in symmetry:

• Line Symmetry:A figure has line symmetry if it can be divided into two congruent halves by a line.
• Point Symmetry:A figure has point symmetry if it can be rotated 180 degrees around a point to create a congruent image.

Applications

Reflections have applications in various fields:

• Architecture:Creating symmetrical designs and mirror images in buildings.
• Design:Creating visually appealing patterns and logos using reflections.
• Physics:Understanding the behavior of light and sound waves through reflections.

FAQ Corner

What is the core concept behind geometric reflections?

Geometric reflections involve flipping a figure across a line, plane, or point, creating a mirror image that retains the original figure’s size and shape.

How are reflections used in geometric constructions?

Reflections serve as fundamental tools in geometric constructions, allowing for the creation of congruent figures, bisecting angles, and constructing perpendicular lines.

What are the different types of symmetry related to reflections?

Reflections play a crucial role in symmetry, contributing to line symmetry, point symmetry, and rotational symmetry, which manifest in various geometric figures and natural forms.